|
5.2.1 ZÁKLADNÉ
ELEKTRICKÉ PARAMETRE VEDENÍ
K základným parametrom elektrických vedení
patria:
R – jednosmerný odpor,
R – činný odpor (rezistancia),
G – zvod,
G – činná vodivosť (konduktancia),
L – indukčnosť,
X – jalový odpor (induktancia),
C – kapacita,
B – jalová vodivosť (susceptancia).
Pri výpočtoch jednosmerných a striedavých
elektrických vedení nízkeho napätia (nn) uvažujeme obvykle len
odpor resp. rezistanciu. Pri vedeniach vysokého napätia (vn)
počítame okrem rezistancie aj s indukčnosťou, počítame s pozdĺžnymi
parametrami R, L, ktoré sú príčinou úbytku napätia. Pri vedeniach veľmi vysokého napätia (vvn) a zvlášť vysokého napätia (zvn)
a káblových vedeniach všetkých napätí počítame aj s kapacitou.
Pri vedeniach nad 60 kV uvažujeme s priečnymi
parametrami G, C,
ktoré sú príčinou úbytku prúdu [101].
5.2.1.1 ODPOR – REZISTANCIA
1. JEDNOSMERNÝ ODPOR
Pre jednosmerné vedenie je odpor ako základný elektrický
parameter na km dĺžky daný vzťahom:
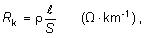
| |
kde je |
Rk |
odpor vodiča dĺžky ℓ = 1 km, |
| |
|
ρ |
merný odpor, |
| |
|
S |
prierez
vodiča. |
Okrem merného odporu sa
často používa jeho prevrátená hodnota merná vodivosť
– konduktivita
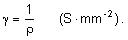
Pre elektrické vedenia je zvykom udávať ich dĺžku v km a prierez
vodiča v mm2. Odpor určitej dĺžky
vedenia ℓ je potom
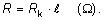
Teplotná závislosť odporu do 100 °C je daná vzťahom
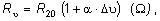
| |
kde je |
R20 |
odpor pri teplote 20 °C, |
| |
|
a |
teplotný súčiniteľ odporu, |
| |
|
u |
teplota, |
| |
|
Du |
oteplenie. |
Izolanty majú mimoriadne vysoký merný odpor,
dosť závislý na teplote. Napr. pre porcelán je to pri 20 °C – 105 Ω·cm
a pri 300 °C – 107 Ω·cm.
2. ČINNÝ ODPOR
Odpor vedenia pre striedavý
prúd nazývame rezistancia a tá
je väčšia ako u vedenia pre jednosmerný prúd, pretože sa
uplatňuje skinefekt. Ten
spôsobuje vytláčanie prúdu smerom k povrchu vodiča, čím sa
zmenšuje využiteľný prierez. Činný odpor je daný vzťahom
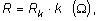
kde k je súčiniteľ rešpektujúci vplyv skinefektu závisiaci od
frekvencie f a priemeru vodiča d. Pre nemagnetický
materiál je
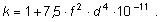
Skinefekt môžme tiež posúdiť tak, že určíme hrúbku povrchovej
vrstvy vodiča, ktorá sa zúčastňuje na vedení striedavého prúdu
tzv. hĺbka vniku
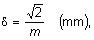
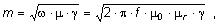
| |
kde je |
g |
merná vodivosť materiálu (S·mm-2·km,) |
| |
|
f |
frekvencia (Hz), |
| |
|
m0 |
permeabilita vákua (H·m-1), |
| |
|
mr |
relatívna permeabilita. |
Pri 50
Hz je hĺbka vniku pre meď 9,5 mm a hliník 12,2 mm. Zvýšenie
odporu vplyvom skinefektu je pri frekvencii 50 Hz malé. Pre
vodiče s prierezom menším ako 150 mm2 je striedavý odpor vodičov
oproti jednosmernému väčší o cca 1 %. Pri hliníkových a
oceľohliníkových lanách dochádza k zväčšeniu striedavého odporu
aj tým, že prúd prekonáva väčšiu vzdialenosť ako je dĺžka lana.
Jednotlivé pramene sú stočené do skrutkovice, pričom ich povrch
je pokrytý nevodivým oxidom. Prúd neprechádza z jedného prameňa
do druhého, ale sleduje dráhu skrutkovice, čím sa odpor zväčší
o cca 1 – 2 % .
3. REZISTANCIA ZEME
Zem ako vodič sa uplatňuje len pri poruchách. Jej rezistanciu
ovplyvňuje len frekvencia. Rezistancia je daná vzťahom
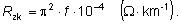
Pre jednosmerný prúd je
rezistancia nulová a uplatňuje sa len odpor uzemňovacích
elektród. Pri 50 Hz je cca 0,05 W·km-1, čo je oproti prechodovej rezistancii
uzemnenia tiež zanedbateľné.
5.2.1.2 ZVOD
Zvod (G) ako základný
elektrický parameter spôsobuje na vedení činné straty, ktoré
závisia na napätí a klimatických podmienkach. Časť z nich vzniká
nedokonalou izoláciou – prechodom zvodového prúdu po povrchu a
vnútrajškom izolátora (vlhko a znečistenie izolátora), časť
vyžiarením do okolia vodiča korónou. Pri káblových vedeniach je
to nedokonalosťou dielektrika (teplota, navlhavosť, vek kábla).
1. ZVODOVÝ PRÚD
Zvodový prúd, ktorý
tečie jednou fázou je
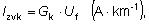
potom straty v jednej fáze
sú
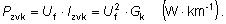
Pri trojfázovom vedení sú straty zvodom
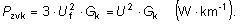
2. KORÓNA
Koróna je
výboj sústredený okolo vodiča a vzniká vtedy, keď intenzita poľa
na povrchu vodiča prekročí hodnotu, pri ktorej začína ionizácia
vzduchu v jeho okolí. Počiatočná hodnota fázového napätia, pri
ktorom vzniká výboj, je kritické napätie koróny
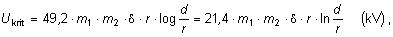
| |
kde je |
m1 |
súčiniteľ drsnosti vodiča (lano 0,85), |
| |
|
m2 |
súčiniteľ počasia (pekne = 1, hmla = 0,8), |
| |
|
d |
relatívna hustota vzduchu, |
| |
|
r |
polomer vodiča (mm), |
| |
|
d |
vzdialenosť fázových vodičov (mm). |
Z uvedeného vyplýva, že
vznik koróny sa dá ovplyvniť voľbou " d " a " r " . Vhodné
vzdialenosti a priemery vodičov, pri ktorých nemá dôjsť ku
koróne, sú v tab. 5.1.
Tab. 5.1. Vzdialenosti a priemery vodičov, pri ktorých nedochádza ku koróne
|
Napätie (kV) |
110 |
220 |
400 |
|
Vzdialenosť vodičov (m)
≥ ako |
3 |
5 |
6 |
|
Priemer vodičov (mm)
≥
ako |
12,5 |
26,5 |
50 |
Vývoj koróny
je sprevádzaný svetelnými a zvukovými efektmi v 3 etapách:
-
nepravidelné sršanie a praskanie, vznikajú
svetielkujúce škvrny,
-
zhustenie a zosilnenie praskania,
svetielkujúce trsy, kríčky,
-
brum a temno modrý svetielkujúci závoj s
ionizovaným vzduchom a ultrafialovým žiarením.
Zvod obyčajne pri bežných výpočtoch neuvažujeme
(počítame s ním od napätia 220 kV a vyššie).
5.2.1.3 INDUKČNOSŤ
Pri odvodení vzťahov pre indukčnosť vedenia
vychádzame zo statickej definície indukčnosti
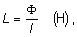
a zo zákona celkového prúdu
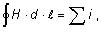
| |
kde je |
F |
magnetický tok (Wb), |
| |
|
I |
prúd (A), |
| |
|
H |
intenzita magnetického poľa (A·m-1), |
| |
|
ℓ |
dĺžka vedenia (m). |
1. Vlastná indukčnosť vodiča dĺžky 1 km je potom daná vzťahom
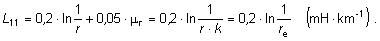
| |
kde je |
r |
polomer vodiča, |
| |
|
k |
súčiniteľ pre výpočet efektívneho polomeru vodiča pre rôzny materiál (0,779 pre plný nemagnetický vodič), |
| |
|
re |
efektívny polomer, ktorý súvisí s konštrukciou vodiča a jeho magnetickými vlastnosťami (0,8 pre AlFe lano). |
Indukčnosť 1 vodiča dvojvodičového vedenia dĺžky 1 km je
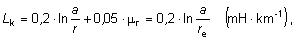
kde a je vzdialenosť vodičov. V literatúre sa často používa
vzťah
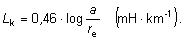
Uvedené vzťahy platia pre indukčnosť jednofázového vedenia, ale
aj pre trojfázové vedenie s vodičmi umiestnenými
vo vrcholoch rovnostranného trojuholníka,
kde sa za a dosadí stredná vzdialenosť vodičov as.
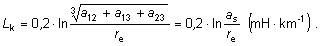
Obr. 5.4. Usporiadanie vodičov dvojitého vedenia (a), trojitého s vodičmi vo vrcholoch
rovnostranného trojuholníka (b) a trojitého s vodičmi vo vrcholoch všeobecného trojuholníka (c)
2. Indukčnosť trojfázového vedenia
Trojfázové vedenie s vodičmi
usporiadanými do všeobecného trojuholníka (obr. 5.4b)
bude mať vzhľadom k rôznym vzdialenostiam vodičov indukčnosť
každého vodiča inú, čo má za následok vznik napäťovej nesymetrie
na vedení napriek súmernosti zdroja a záťaže.
Ak chceme vzniku takejto
nesymetrie zabrániť, musíme polohu vodiča po určitých úsekoch
navzájom vystriedať – transponovať. Možné
spôsoby vystriedania vodičov sú uvedené na obr. 5.5 a 5.6. Ak
každý vodič zaujme na rovnakých úsekoch všetky tri polohy, potom
bude indukčnosť každého vodiča rovná strednej hodnote
indukčnosti všetkých vodičov.
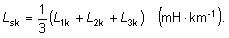
Pretože L11=L22=L33, môžeme vlastnú indukčnosť označiť L a vzťah pre
indukčnosť jednotlivých vodičov bude
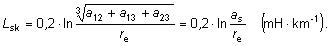
Miesto výmeny polohy vodičov na vedení sa nazýva zákrut. Zákruty
môžu byť úplné (všetky vodiče zmenia svoju polohu), alebo
čiastočné (len dva vodiče zmenia svoju polohu). Vedenia môžu mať
v praxi rôzny počet zákrutov. Nevýhodou pri striedaní fáz je, že
na konci vedenia nie sú fázy v rovnakom poradí ako na začiatku
(obr. 5.5). Dá sa to odstrániť pridaním jedného zákrutu navyše
(obr. 5.6).
 Obr. 5.5. Transpozícia vedenia – sled fáz na začiatku a na konci je iný
 Obr. 5.6. Transpozícia vedenia – sled fáz na začiatku a na konci je rovnaký
V sieťach vn sa z ekonomických dôvodov transpozícia nerobí
(drahý zákrutový stožiar). Vo vvn sieťach sa v minulosti robil
zákrut na každých 30 km. V súčasnosti je napr. na Slovensku 14
transponovaných vedení vvn a zvn so zákrutmi na každých 40 až 80
km dĺžky.
 Obr. 5.7. Transpozičný stožiar [149]
3. Indukčnosť vedenia so zväzkovými vodičmi
Pre zmenšenie indukčnosti vedenia,
ale hlavne kvôli obmedzeniu strát korónou, sa pre vedenia vvn a zvn
používajú zväzkové vodiče. Je to systém lán elektricky
a mechanicky spojených rozperkami, ktoré udržujú vodiče
mechanicky od seba a správajú sa tak, ako keby išlo o vodič
s polomerom
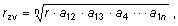
| |
kde je |
r |
polomer jednotlivého vodiča, |
| |
|
a1n |
vzdialenosti vodiča 1 od vodiča n vo zväzku, |
| |
|
n |
počet vodičov vo zväzku. |
Indukčnosť vedenia so zväzkovými
vodičmi je daná vzťahom
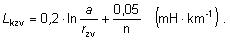
Vzdialenosť vodičov vo zväzku sa pohybuje medzi 50 – 60 cm.
Počet vodičov vo zväzku závisí na napäťovej hladine, pre 220 kV
sa používa dvojzväzok, pre 400 kV trojzväzok.
Napr. pre 220 kV je dvojzväzok
drahší asi o 21 %, reaktancia vedenia je však menšia o 25 % a
prenosová schopnosť sa zvýši o 30 %. Reaktancia vzdušného
vedenia jedného vodiča je 0,4 Ω·km-1, dvojzväzku 0,3 Ω·km-1
a trojzväzku 0,25 Ω·km-1.
4. Indukčnosť káblových vedení
Pri káblových vedeniach závisí vzťah pre
výpočet na type kábla. Pre trojžilový kábel s vodičmi kruhového
prierezu bez kovového obalu je vzorec rovnaký ako pre vonkajšie
vedenie.
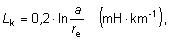
| |
kde je |
a |
vzdialenosť osí vodičov, |
| |
|
re |
ekvivalentný polomer žily. |
Pretože a je malé, je indukčnosť
kábla s kruhovými vodičmi podstatne menšia ako vonkajšieho
vedenia (u kábla so sektorovými žilami je ešte o 5 až 10 %
menšia).
Jednožilový kábel s kovovým obalom
alebo trojplášťový kábel má indukčnosť
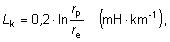
kde
rp je vnútorný polomer plášťa.
5.2.1.4 KAPACITA
Vzťah medzi nábojom Q, kapacitou C a
potenciálom V opisuje rovnica
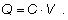
Potenciál je
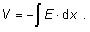
Ak uvažujeme 2 body v elektrickom
poli vodiča, v kolmých vzdialenostiach x1 a x2 od osi vodiča,
je medzi nimi potenciálový rozdiel
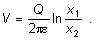
Výsledné potenciály vodičov v elektrickom poli sa skladajú
z vlastného a vzájomného potenciálu, ktoré závisia len na
polomere a geometrickom usporiadaní vodičov.
1. Kapacita trojfázového vedenia
Jednotlivé vodiče viacvodičového
vedenia majú kapacitu
voči zemi, ktorú podľa obr. 5.9 označujeme „k“
a kapacity voči ostatným vodičom, ktoré označujeme „k´“ a nazývajú
sa čiastkové kapacity.
Kapacity voči zemi a medzi vodičmi tvoria celkovú alebo prevádzkovú kapacitu vodiča.
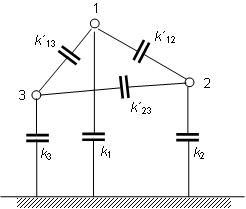 Obr. 5.9. Kapacity trojfázového vedenia
Celková prevádzková kapacita
jedného vodiča trojfázového vedenia za predpokladu, že k1 = k2 = k3 = k, k'12 = k'23 = k'13 = k' bude
Cp =
k + 3 k´ .
2. Kapacita dvojvodičového vedenia
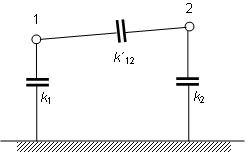 Obr. 5.10. Čiastkové kapacity dvojvodičového vedenia
Pre dvojvodičové vedenie platí podľa obr. 5.10 pre prevádzkovú
kapacitu vodiča
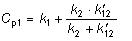
a pre transponované vodiče
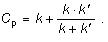
Uvedené vzťahy platia aj pre kapacity vedení so zväzkovými
vodičmi, len za polomer musíme dosadiť náhradný polomer zväzku
rzv. U vedení so zemnými lanami ovplyvňuje zemné lano kapacity
medzi vodičmi, ale výslednú kapacitu neovplyvňuje (má nulový
potenciál a čiastkovú kapacitu proti zemi).
3. Kapacita káblového vedenia
Kapacita
káblových vedení závisí na ich konštrukčnom usporiadaní a na
permitivite použitého izolačného materiálu. Káble jednožilové a
viacžilové s kovovým plášťom pre každú žilu majú len kapacitu
proti tomuto plášťu a táto kapacita je zároveň prevádzkovou
kapacitou. Je daná vzťahom
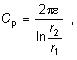
| |
kde je |
r1 |
polomer žily, |
| |
|
r2 |
polomer vnútornej plochy kovového plášťa. |
Po dosadení za ε0 = 8,8541
nF·km-1 a úprave dostaneme
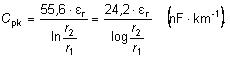
Trojžilové káble so spoločným kovovým plášťom sa z hľadiska
kapacity správajú ako symetrizované trojfázové vzdušné vedenie,
pri celoplástových kábloch závisí kapacita aj na spôsobe
uloženia. Vo všeobecnosti je kapacita káblov oveľa vyššia ako
kapacita vonkajších vedení (cca 10 krát).
5.2.2 STRIEDAVÉ VEDENIA A SIETE
Trojfázové vedenia a siete nn a vn
Tieto vedenia
sa používajú pre zásobovanie priemyslu, poľnohospodárstva,
elektrickej vozby mestskej a železničnej, menších miest a dedín.
Pri výpočtoch sa vychádza z predpokladu, že sústava je súmerná
a všetky napätia a prúdy majú harmonický priebeh. Pozdĺžna
impedancia je konštantná po celej dĺžke vedenia a priečna
admitancia sa zanedbáva. Pri sieťach nn sa môže tiež zanedbať
reaktancia.
Pri výpočtoch
uzlových sietí vn sa zisťujú predovšetkým prúdové a napäťové
pomery v jednotlivých vedeniach a uzloch pri normálnych
podmienkach a pri typických poruchách siete. Najvhodnejšia
metóda pre výpočty je metóda uzlových napätí. Vzhľadom na
predpoklad symetrie sústavy stačí vypočítať prúdy a napätia pre
jednu fázu s tým, že výsledky v ostatných fázach sú rovnaké, ale
len pootočené o 120 resp. 240 stupňov.
Trojfázové vedenia a siete vvn a zvn
Vedenia vvn sa používajú pre zásobovanie veľkých
spotrebiteľov, striedavej elektrickej vozby, veľkých miest a sú
aj súčasťou distribučnej a prenosovej sústavy. Slúžia tiež na
prepojenie so zahraničím.
Pri výpočtoch sa vychádza z predpokladu, že
vedenia sú súmerné a všetky napätia a prúdy majú harmonický
priebeh. Pozdĺžna impedancia a priečna admitancia sú konštantné
po celej dĺžke vedenia. Vzhľadom na predpoklad symetrie sústavy
stačí vypočítať prúdy a napätia pre jednu fázu s tým, že
výsledky v ostatných fázach sú rovnaké, ale len pootočené o 120
resp. 240 stupňov. Výpočty môžu byť vykonané dvoma metódami:
5.2.2.1 Výpočet vedenia s rovnomerne rozloženými parametrami
Pri tomto type výpočtov predpokladáme líniové
vedenie a parametre R, L, C, G rovnomerne rozložené po jeho
celej dĺžke pričom sa nemenia (homogenné
vedenie). Napätie a prúd sú funkciou miesta a času. Pri
známych hodnotách fázového napätia a prúdu na začiatku vedenia
sa hodnoty na konci vypočítajú podľa vzťahov
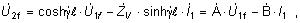
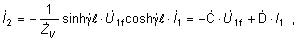
kde
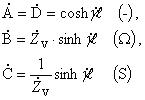
sú Blondelove konštanty dlhého vedenia
a platí pre ne vzťah
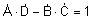 ˙ ˙
Merná komplexná miera prenosu
a vlnová impedancia
sú dané vzťahom
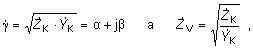
| |
kde je |
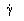 |
– merná komplexná miera prenosu (km-1), |
| |
|
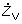 |
– vlnová impedancia (W·km-1), |
| |
|
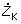 |
– pozdĺžna impedancia nakrátko (W·km-1), |
| |
|
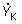 |
– priečna impedancia nakrátko (S·km-1), |
| |
|
α |
– merná miera tlmenia (dB·km-1), |
| |
|
β |
– merná miera fázového posunu (rad·km-1), |
5.2.2.2 Výpočet vedenia s náhradnými článkami
Parametre vedenia sú u tejto metódy sústredené
do jedného miesta. Náhradný článok predstavuje dvojbran v tvare
π - článku (obr. 5.11), T - článku (obr. 5.12) alebo Γ - článku
(obr. 5.13). V článkoch je
pozdĺžna impedancia
Ż = R + jωL a priečna admitancia
Ÿ = G + jωC.
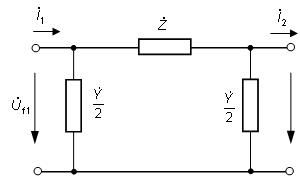 Obr. 5.11. Náhradný
π - článok dlhého vedenia
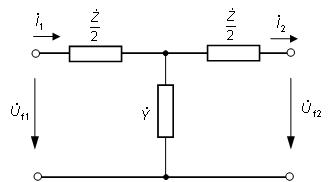 Obr. 5.12. Náhradný T - článok dlhého vedenia
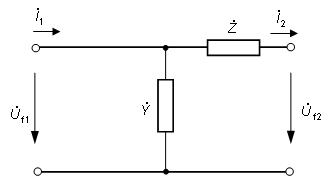 Obr. 5.13. Náhradný Γ - článok dlhého vedenia
V tab. 5.2 sú uvedené Blondelove konštanty dlhého vedenia pre jednotlivé spôsoby výpočtu fázového napätia a prúdu na začiatku vedenia,
ak poznáme hodnoty na jeho konci. Náhradný π-článok a T-článok sa používa pre výpočty vonkajšieho vedenia dĺžky do 300 km a káblového
do 100 km. Náhradný Γ-článok sa používa pre výpočty vonkajšieho vedenia do dĺžky 100 km a káblového do 25 km. Tab. 5.2. Blondelove konštanty
|
Spôsob riešenia |
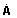 |
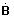 |
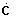 |
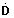 |
|
homogenné vedenie |
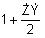 |
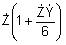 |
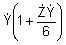 |
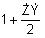 |
|
π - článok |
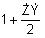 |
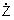 |
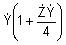 |
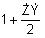 |
|
T - článok |
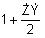 |
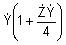 |
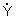 |
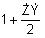 |
|
Γ - článok |
1 |
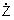 |
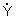 |
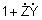 |
5.2.2.3 Výkony v trojfázových sústavách
V striedavých sústavách dochádza vplyvom záťaže
k fázovému posunu medzi časovými priebehmi prúdu a napätia
o uhol φ, obr. 5.14.
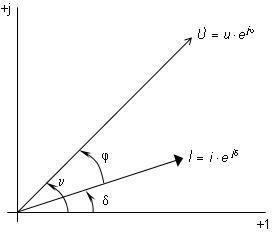 Obr. 5.14. Fázorový diagram prúdu a napätia pri záťaži induktívneho charakteru
V trojfázových striedavých sústavách sú definované nasledujúce
výkony:
| |
zdanlivý výkon jednofázový |
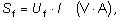 |
| |
zdanlivý výkon trojfázový |
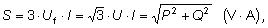 |
| |
činný výkon jednofázový |
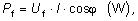 |
| |
činný výkon trojfázový |
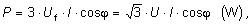 |
| |
jalový výkon jednofázový |
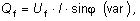 |
| |
jalový výkon trojfázový |
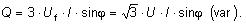 |
Vo vzťahoch sú Uf a I fázové hodnoty napätia
a prúdu, U je združené napätie a φ je fázový posun medzi
napätím a prúdom.
5.2.2.4 Zvláštne prípady prenosov
Vedenie zakončené vlnovou impedanciou
Na vedení zakončenom impedanciou Ż2 = ŻV neexistujú odrazy a platí
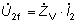 ˙ ˙
Prúd a napätie majú len postupnú vlnu a ich
pomer je v každom mieste rovný veľkosti vlnovej impedancie.
Z hľadiska prenosu energie
tento stav je
optimálny a preto sa v prevádzke vždy snažíme
čo najviac sa k nemu priblížiť, predovšetkým pri prenosoch na
veľké vzdialenosti. Prúd, ktorý preteká vedením zakončeným
vlnovou impedanciou, sa nazýva
prirodzený prúd
a prenášaný výkon sa nazýva
prirodzený výkon.
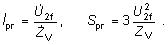
Vedenie naprázdno
Z vedenia pracujúceho naprázdno nie je odoberaný
žiadny výkon a platí
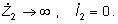
Vstupná impedancia vedenia potom bude
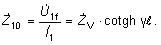
Pri stave naprázdno prechádza vedením
nabíjací prúd,
ktorý uzaviera kapacitu vedenia Cpk. Na začiatku
vedenia je nabíjací prúd maximálny, lineárne klesá a na konci
vedenia je nulový.
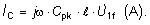
Nabíjaciemu prúdu zodpovedá
nabíjací výkon,
ktorý odoberá vedenie zo sústavy.
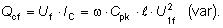
Kapacitný nabíjací prúd spôsobuje zmenu napäťových pomerov vo
vedení naprázdno. Prejaví sa to zvýšením napätia na konci
vedenia oproti začiatku. Táto skutočnosť sa nazýva
Ferrantiho jav
a ten je z prevádzkového hľadiska veľmi nepriaznivý. Napríklad
pri poruche a náhlom odpojení záťaže na dlhom vedení môže dôjsť
k prierazu izolácie.
Vedenie nakrátko
Pri tomto stave
je vedenie na konci skratované a platí:
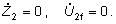
Vstupná impedancia vedenia potom bude
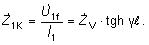
Zo vstupných impedancií vedenia pri stave naprázdno a nakrátko
sa tiež vypočíta vlnová impedancia
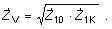 Tab. 5.3. Informatívne hodnoty vlnovej impedancie a prirodzeného výkonu
|
Vedenie |
Počet vodičov na fázu |
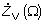 |
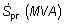 |
|
6 kV káblové |
1 |
20
– 50 |
0,7
– 1,8 |
|
22 kV káblové |
1 |
40
– 80 |
6 –
12 |
|
22 kV vonkajšie |
1 |
420
– 540 |
0,9
– 1,2 |
|
110 kV vonkajšie |
1 |
370
– 400 |
30
– 33 |
|
220 kV vonkajšie |
1 |
390 |
120 |
|
400 kV vonkajšie |
3 |
280 |
580 |
5.2.3 JEDNOSMERNÉ
VEDENIA A SIETE
V súčasnosti
majú jednoduché jednosmerné
vedenia len obmedzené použitie pre rozvody elektrickej energie.
Používajú sa napríklad pre napájanie núdzového osvetlenia a
náhradných zdrojov. Rozvod býva dvojvodičový, alebo jeden pól
môže byť uzemnený. Výrazné použitie majú jednosmerné siete v
elektrickej vozbe a technologických procesoch,
v priemyselných pohonoch, v metalurgickom a chemickom priemysle.
Obnovenie používania jednosmerných prenosov v elektrizačných
sústavách v poslednej dobe našlo uplatnenie najmä pre:
-
prepojenie dvoch sústav s rôznymi frekvenciami ako
jednosmerné spojky,
-
reguláciu prenášaného výkonu
medzi sústavami,
-
prenos veľkých výkonov na veľké vzdialenosti,
-
dlhé podmorské káblové
vedenia,
-
zvýšenie prenosovej schopnosti sústavy, ktorej prenosová schopnosť je obmedzená
stabilitou paralelného chodu generátorov.
Jednosmerné prenosy prinášajú tieto výhody:
-
náklady na výstavbu stožiarov a vodičov sú menšie (nižšie
stožiare, len dva vodiče),
-
ako spätný vodič sa môže použiť zem,
-
nie je skinefekt,
-
nie sú dielektrické a hysterézne straty a straty vírivými
prúdmi,
-
existuje jednoduchá regulácia veľkosti a smeru toku
výkonu,
-
používajú jednoduchšiu izoláciu a tým majú možnosť
použitia vyššieho napätia,
-
úbytok napätia je menší než pri striedavom prenose,
-
prenosová schopnosť je väčšia ako pri striedavom
prenose,
-
menšie straty oproti stratám v striedavých sieťach,
-
koróna vzniká až pri vyššom napätí.
Nevýhody jednosmerných prenosov sú:
-
nákladné usmerňovače a striedače,
-
pri použití zeme ako vodiča vznikajú bludné
prúdy a elektrochemická korózia.
Po všetkých technických stránkach je jednosmerný
prenos výhodnejší než striedavý, ale má väčšie investičné
náklady.
a) Vedenie napájané z jednej strany
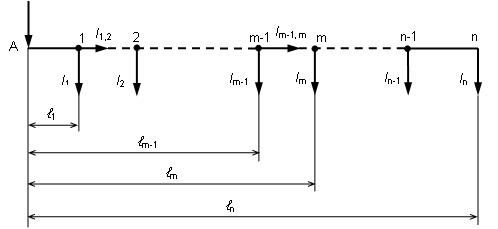 Obr. 5.15. Jednosmerné vedenie napájané z jednej strany
Predpokladáme, že vedenie je dvojvodičové, obidva vodiče sú z
rovnakého materiálu, s identickým merným odporom r a prierezom
S. Úbytok napätia na konci vedenia sa môže počítať dvoma
spôsobmi:

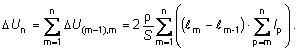
Straty na jednosmernom vedení sú dané súčtom strát
v jednotlivých úsekoch
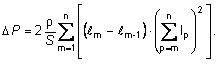
b) Vedenie napájané z dvoch strán rovnakým napätím
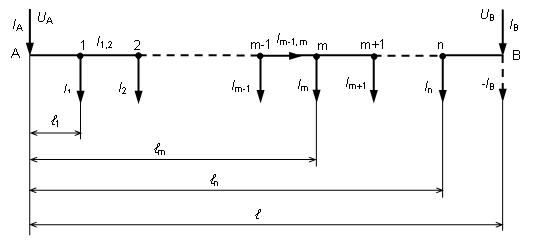 Obr. 5.16. Jednosmerné vedenie napájané z dvoch strán
Pri riešení postupujeme tak, že prúd dodávaný z napájača B
uvažujeme ako záporný odber
- IB a
problém prevedieme na jednostranne napájané vedenie. Úbytok
napätia medzi napájačmi A a B považujeme za nulový (UA
= UB). Potom môžme vypočítať úbytok na vedení
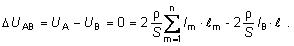
Prúd dodávaný z napájača B potom bude
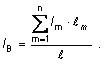
V prípade, že vedenie je napájané z dvoch strán rôznym napätím,
riešime jeho napájanie metódou superpozície a uvažujeme s
vyrovnávacím prúdom
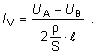 |